KEPLERO


IL Mysterium Cosmographicus di Keplero 

(le parti in blu derivano da http://it.wikipedia.org/wiki/Keplero)

Keplero fu capace di dedurre le sue leggi sui pianeti senza conoscere le esatte distanze dei pianeti dal Sole, poiché le sue analisi geometriche richiedevano solo il rapporto tra le rispettive distanze dal Sole. Secondo Keplero, luce, calore, moto, armonia dei moti sono la perfezione del mondo e hanno un analogo nelle facoltà dell'anima. Le stelle fisse funzionano come una "pelle" protettiva che trattiene il calore del Sole. Questi è la causa del moto dei pianeti, poiché ruotando su di sé, trascina gli altri corpi. La potenza vegetativa dell'etere corrisponde alla nutrizione di animali e piante, alla facoltà vitale corrisponde il calore, a quella animale il movimento, alla sensitiva la luce e alla razionale l'armonia.
Keplero, a differenza di Tycho Brahe, appoggiò il modello eliocentrico del sistema solare e partendo da questo per vent'anni provò a dare un senso ai suoi dati. Alla fine giunse a formulare le sue tre leggi sui movimenti planetari che enunciò nelle tavole rudolfine.
Mentre le prime due leggi furono enunciate in un classico libro di astronomia, la terza, invece, fu inserita in un testo che si occupava anche di musica e di astrologia e che era denso di temi pitagorici. Keplero, convinto che Dio non fosse solo geometra ma anche un musico, sostenne l'idea che la musica e il sistema solare fossero manifestazioni della stessa armonia; quasi come se le posizioni dei vari pianeti, similmente ai tasti di un pianoforte, dovessero corrispondere alle note.
Keplero è una figura ingombrante collocata tra Galilei e Newton. Fortemente interessato a tematiche mistiche e metafisiche di natura platonica e pitagorica, la sua "modernità" consiste nella ricerca delle variazioni quantitative delle forze che agiscono nello spazio e nel tempo e nel parziale abbandono del punto di vista animistico in favore di un meccanicismo allo stato embrionale. La terza legge permette di stabilire la velocità del corpo celeste una volta stabilita l'orbita e viceversa. Si era scoperta una legge che non regolava semplicemente i moti dei pianeti nelle proprie orbite, ma si stabiliva un rapporto tra la velocità dei corpi che si muovono in orbite differenti. Galilei si congratulò con lui per avere accolto il Copernicanesimo ma non si pronunciò sul resto, aggiungendo che alcuni dei suoi pensieri fossero "piuttosto a diminuzione della dottrina del Copernico che a stabilimento" (Galilei). Bacone, pur essendo molto legato alla tradizione ermetica, lo ignorò e Cartesio lo riconobbe come il suo primo maestro di ottica, non considerando il resto come degno di attenzione. Solo dopo che Newton si servì delle leggi di Keplero, queste vennero accettate dalla comunità scientifica, ma non prima degli anni sessanta del Seicento.

..................................................

Le "armonie celesti" di Keplero
da "Uomo di scienza. Uomo di fede"

di Mario Gargantini

Chi ha mai detto che una visione metafisica o addirittura mistica non possa offrire spunti preziosi per il procedere della ricerca scientifica?
Non ci riferiamo al taoismo e alle filosofie orientali, oggi tanto di moda tra i fisici; in questi casi, più che fornire suggerimenti all'indagine scientifica, la filosofia svolge la funzione di copertura e di pronto soccorso epistemologico per superare (apparentemente) i colli di bottiglia in cui la fisica subnucleare si è infilata.
Vogliamo piuttosto ritornare a quel tormentato periodo, passato alla storia con il termine di «rivoluzione scientifica» ma vissuto dai protagonisti in modo ben poco rivoluzionario. È il caso anche di Giovanni Keplero, uno dei primi e autorevoli
sostenitori della cosmologia copernicana.


Tra Platone...
Vissuto, come Galileo, a cavallo tra il 1500 e il 1600, in una terra travagliata come la Germania, risente più che mai di tutte le difficoltà ideologiche e spirituali dell'epoca; riuscendo tuttavia a trasformare quel ribollire di tendenze contraddittorie
in ricchezza di immagini e di idee.
La sua prima delle tre ben note leggi, quella che colloca la Terra su di un'orbita ellittica con il Sole in uno dei fuochi, è forse altrettanto «rivoluzionaria» quanto l'ipotesi eliocentrica di Copernico. Lo stesso abate polacco, come pure Galileo, non avevano osato intaccare il dogma platonico della circolarità dei moti celesti, simbolo di uniformità e di perfezione. Keplero invece non esita a infrangere la barriera, forte di quell'attaccamento ai dati delle osservazioni assimilato negli anni di collaborazione con il grande astronomo Tycho Brahe.
Come pure non evita di porsi in contrasto con Galileo sulla questione delle maree, facendosi accusare da quest'ultimo di aver «prestato fede a delle proprietà occulte e altre simili fantasie».
In entrambi i casi aveva ragione lui; ma ci volle più di un secolo, e il genio sintetico di Newton, per dimostrarlo.
A dispetto di queste posizioni progressiste, l'«humus » culturale di Keplero era imbevuto di tradizione classica. A partire proprio da Piatone.
È evidente il riferimento al filosofo greco nella ardita costruzione del modello
kepleriano di sistema solare. Keplero non possedeva ancora la chiave
interpretativa dei moti planetari (che verrà fornita dalla legge di Newton);
d'altra parte doveva pur spiegarsi come mai i pianeti obbedissero
alle sue tre leggi, ricavate dalle osservazioni empiriche.
Ecco allora il ricorso a Platone, alla stupefacente architettura del cosmo,
disegnata nel Timeo e basata sui cinque poliedri regolari.
Nel Mysterium Cosmographicum, lo scienziato tedesco costringe le orbite
planetarie su sfere concentriche inscritte e circoscritte nei cinque
solidi platonici: cubo, tetraedro, pentadodecaedro, icosaedro e ottaedro.
Ma non si tratta di pura ipotesi fantastica: Keplero, come tutti i nuovi fisici,
era anzitutto un matematico e prima di proporre il suo modello aveva
«calcolato»: ebbene, il fatto sorprendente è che i rapporti tra i raggi dei
pianeti desunti dalle osservazioni dirette si adattano assai bene ai rapporti
ricavati dalla pura costruzione geometrica.
Oggi sappiamo che ciò non basta per stabilire una legge fisica:
ci vuole la controprova dell'esperimento.
Lo sforzo di Keplero rese tuttavia sintomatico di un momento di passaggio dove l'insopprimibile tentazione dell'uomo di fantasticare inizia a sottoporsi al rigore della matematica e ad obbedire al responso degli strumenti di osservazione.
Peraltro alcuni commentatori hanno sottolineato il carattere apertamente allegorico e simbolico del Mysterium Cosmographicum, che lo avvicina ancor di più al Timeo platonico. Conservando alcuni simboli antichi, l'autore li traduce nella visione cristiana (Keplero era protestante): così il pentadodecaedro, che per Platone simboleggiava la bellezza dell'intero universo, qui racchiude l'orbita della Terra e quindi l'uomo «fine di ogni creazione». Come pure la simmetria platonica è conservata ponendo la Terra in mezzo ai pianeti.
Forse Keplero non sarebbe neppure stato troppo disturbato dalle affermazioni di Arthur Koestler che ha bollato questo suo lavoro come «pseudo-scoperta»: più forte era l'esigenza di evitare la divaricazione forzata tra le implacabili strade della scienza quantitativa e la potente visione del mondo fondata sull'ipotesi di un Creatore buono.
Certo non si può non essere d'accordo con Poincaré quando afferma che
«questa idea non conteneva nulla di assurdo ma era sterile, dal momento
che la natura non è fatta così».


...e Pitagora
Sterile però non si è rivelata la convinzione, già dei pitagorici, che «Dio geometrizza sempre».
Convinzione abbracciata entusiasticamente da Keplero al punto di fargli scrivere un grande trattato sull'Armonia del mondo (Harmonices mundì). E se i greci hanno coniato il termine cosmo, che significa bellezza oltre che ordine, la scienza di tutti i tempi ha trovato nella geometria lo strumento concettuale per dare alla bellezza anche un supporto oggettivo e rigoroso.
I fisici e i biologi moderni macinano nei loro computer miliardi di numeri per trovare nuove simmetrie e nuove strutture da applicare ai fenomeni naturali; la stessa cosa ha fatto Keplero, con gli strumenti allora disponibili.
E, sulla scia di Pitagora, ha visto nelle armonie musicali il paradigma di tutta la realtà. La ragione di ciò sta in una analogia cosmica che vedrebbe riflessa in tutti i fenomeni la precisa armonia dei rapporti geometrici esistente tra i corpi celesti e impressa dal Creatore all'universo come un codice genetico.


L'analogia trinitaria
E sterile non si è rivelata neppure l'analogia trinitaria, la più scandalosa agli occhi illuminati dei moderni, se ha portato Keplero a difendere per primo pubblicamente l'ipotesi copernicana e a trovare spunti per le tre leggi; le quali restano valide anche nell'era della relatività e dei viaggi spaziali. La preferenza di Keplero per un universo eliocentrico piuttosto che geocentrico era espressamente di origine metafisica.
«Io cercherò questa analogia nella mia futura opera cosmografica... Il Sole nel mezzo degli astri mobili, lui stesso immobile e pertanto sorgente di movimento, è l'immagine del Creatore di Dio Padre.
Egli distribuisce la sua forza motrice attraverso un mezzo che contiene i corpi in movimento, allo stesso modo che Iddio Padre crea attraverso lo Spirito Santo».
Quindi Sole, astri e spazio interstellare come Padre, Figlio e Spirito Santo.
È a partire da una visione così imbevuta di medioevale atteggiamento apologetico che Keplero arriva alle conclusioni più moderne Giungendo, nell'Astronomia Nova, a sfiorare il principio della gravitazione universale newtoniana, probabilmente troppo in anticipo sui tempi della storia.
E anticipando una visione della attrazione tra i corpi molto più vicina al concetto di «campo», con cui i fisici moderni descrivono tutte le diverse interazioni: gravitazionali, elettro-magnetiche e nucleari.


Le sorgenti della scienza 
La scienza è cresciuta anche per opera di gente come Keplero, con tutto il suo misticismo e le sue «fantasie».
Il secolo dei lumi, che tanto si è vantato di aver portato a compimento la rivoluzione scientifica, ha ignorato la sorgente dell'ispirazione di tanti grandi scienziati: forse per non dover ammettere che tale sorgente era la visione cristiana della vita e della storia. Così, nella sua «arroganza razionalista», come la chiama Koestler, ci ha tramandato una storia monca, privata degli inizi delle più belle avventure. E, quel che è peggio, ha abituato storici e scienziati a sottovalutare gli inizi. Al punto da indurre uno spirito
sensibile come Einstein a cedere al luogo comune dichiarando (1952) che «Keplero era un protestante devoto» ma il suo successo scientifico dipendeva dall'essersi «liberato in grande misura dalla tradizione spirituale in cui era nato».
Se è vero che la scienza contemporanea soffre di una crisi di legittimità, personaggi come Keplero e gli scienziati suoi contemporanei costituiscono una provocazione e una testimonianza preziosa, soprattutto sul piano degli atteggiamenti e dell'impostazione di partenza.
Dopo l'ubriacatura positivista e neo-positivista, gli scienziati si sono trovati a corto di « ragioni » che possano giustificare la fatica della ricerca: si sono accorti che per conoscere la realtà non basta avere un metodo, per quanto raffinato: ci vuole soprattutto un «movente», un desiderio, una aspettativa, che trascenda il semplice risultato scientifico e resista alla difficoltà e all'insuccesso. I giovani oggi non hanno difficoltà ad apprezzare l'efficacia del metodo sperimentale né ad assimilarne i procedimenti: più difficile è convincerli che può valere la pena dedicare il proprio lavoro allo studio di oggetti lontani miliardi di anni luce, come le galassie, o contenuti in miliardesimi di metro come i frammenti del Dna.
Keplero aveva ereditato dai secoli precedenti «la sorgente» da cui può sgorgare la linfa della conoscenza.
Una sorgente, come tutte, che si fa strada in mezzo al fango, che sgorga tra le pietre e trascina con sé.

(a cura di Umberto De Palma)

............................................................................................................

............................................................................................................

(a cura di Domenico Ruggiero)

Le tre leggi del movimento dei pianeti sono il principale contributo di Johannes Kepler, detto Keplero, all'astronomia e alla meccanica. Keplero le derivò in parte studiando le osservazioni di Tycho Brahe. Isaac Newton avrebbe più tardi verificato la validità di queste leggi alla luce della teoria della gravitazione universale.

Prima legge (1608)

La prima legge afferma che:

Keplero propone un modello eliocentrico in cui non vengono più considerate le orbite circolari, le forme perfette, ed è supportato nel farlo dai dati sperimentali ottenuti da Tycho Brahe. Osserviamo che, poiché l'ellisse è una figura piana, i moti dei pianeti avvengono in un piano, detto piano orbitale. Per la Terra tale piano è detto eclittica. Nella figura a fianco è rappresentata un'orbita ellittica, con indicati i suoi parametri caratteristici: semiasse maggiore (a), semiasse minore (b), semi-distanza focale (c), eccentricità (e).
Tra questi parametri esistono le relazioni seguenti:

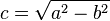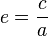
L'ellisse in figura ha un'eccentricità di circa 0,5 e potrebbe rappresentare l'orbita di un asteroide. I pianeti hanno in realtà eccentricità molto più piccole: 0,0167 per la Terra, 0,0934 per Marte e 0,2482 per Plutone (pianeta nano).
La distanza dei pianeti dal Sole non è costante, ma varia da un massimo (afelio) ad un minimo (perielio). È possibile considerare la prima legge di Keplero collegata alla conservazione del momento angolare.

...........................................................................................

Seconda legge (1609) - Legge delle aree 

« Il segmento (raggio vettore) che unisce il centro del Sole con il centro del pianeta descrive aree uguali in tempi uguali. »

La seconda legge afferma che:

Le conseguenze di questa legge sono:

• La velocità areolare è costante.

• La velocità orbitale non è costante, ma varia lungo l'orbita. Le due aree evidenziate nella figura qui a fianco sono infatti uguali e vengono quindi percorse nello stesso tempo. In prossimità del perielio, dove il raggio vettore è più corto che all'afelio, l'arco di ellisse è corrispondentemente più lungo. Ne segue quindi che la velocità orbitale è massima alperielio e minima all'afelio.

• Il momento angolare orbitale del pianeta si conserva (vedi riquadro sotto per la dimostrazione).

• La velocità lungo una determinata orbita è inversamente proporzionale al modulo del raggio vettore. Questa è una conseguenza della conservazione del momento angolare. Se L, dato dal prodotto di m, r e v_t è costante ne discende che v_t è inversamente proporzionale a r (si veda "momento angolare" per la definizione di L, m, r e v_t).

• Sul pianeta viene esercitata una forza centrale, cioè diretta secondo la congiungente tra il pianeta e il Sole. La seconda legge della dinamica per i sistemi in rotazione è
  
  
  
  dove M è il momento meccanico applicato. Poiché L si conserva, la sua variazione è nulla e quindi anche M è nullo. Questo può accadere solo se F è parallelo ad r, cioè è diretto come la congiungente con il Sole.

La seconda legge di Keplero risulta quindi generalizzabile ad un qualsiasi moto centrale, legando l'accelerazione tangenziale alla velocità areolare. Nella figura qui a fianco OA rappresenta il raggio vettore e AB la traiettoria del pianeta nel tempo Δ t. Se Δ t è sufficientemente piccolo, AB può essere approssimato da un segmento di retta. Sia inoltre θ l'angolo tra il raggio vettore e AB.

 

Nel tempo Δ t viene quindi descritta un'area .
La velocità areolare è quindi , essendo 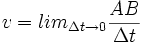 la velocità orbitale istantanea. Poiché m v r sin(θ) è il modulo del momento angolare, risulta 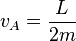. Se v_A è costante, anche L lo è.












..........................................................................................................

Terza legge (1619) 

La terza legge afferma che:

« I quadrati dei periodi di rivoluzione dei pianeti sono proporzionali ai cubi dei semiassi maggiori delle loro orbite. »

Questa legge è valida anche per i satelliti che orbitano intorno ai pianeti e può essere espressa in forma matematica nel modo seguente:

 

dove a è il semiasse maggiore (o equivalentemente il raggio medio) dell'orbita, T il periodo di rivoluzione e K una costante (a volte detta di Keplero), che dipende dal corpo celeste attorno al quale avviene il moto di rivoluzione (ad esempio, se si considera il moto di rivoluzione dei pianeti del sistema solare attorno al Sole e misurando le distanze in U.A. e il tempo in anni solari, K vale 1). Per un'orbita circolare la formula si riduce a

 

dove r è il raggio dell'orbita.

Si può dimostrare che 

con 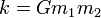 per il caso gravitazionale e  massa ridotta.

 

Limiti di validità delle leggi di Keplero

Va specificato che le leggi di Keplero sono precise nella misura in cui sono soddisfatte le seguenti ipotesi:

- la massa del pianeta è trascurabile rispetto a quella del Sole;

- si possono trascurare le interazioni tra diversi pianeti (tali interazioni portano a leggere perturbazioni sulla forma delle orbite.




(da wikipedia)